This tutorial consists of two parts: the first part will describe how to ray trace one sphere using OpenCL, while the second part covers path tracing of a scene made of spheres. The tutorial will be light on ray tracing/path tracing theory (there are plenty of excellent resources available online such as Scratch-a-Pixel) and will focus instead on the practical implementation of rendering algorithms in OpenCL.The end result will be a rendered image featuring realistic light effects such as indirect lighting, diffuse colour bleeding and soft shadows, all achieved with just a few lines of code:
Part 1: Ray tracing a sphere
Computing a test image on the OpenCL device
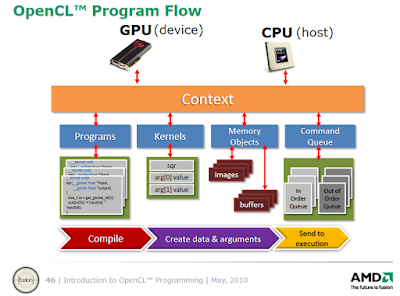
The host (CPU) sets up the OpenCL environment and launches the OpenCL kernel which will be executed on the OpenCL device (GPU or CPU) in parallel. Each work item (or thread) on the device will calculate one pixel of the image. There will thus be as many work items in the global pool as there are pixels in the image. Each work item has a unique ID which distinguishes from all other work items in the global pool of threads and which is obtained with get_global_id(0).
The X- and Y-coordinates of each pixel can be computed by using that pixel's unique work item ID:
- x-coordinate: divide by the image width and take the remainder
- y-coordinate: divide by the image width
By remapping the x and y coordinates from the [0 to width] range for x and [0 to height] range for y to the range [0 - 1] for both, and plugging those values in the red and green channels repsectively yields the following gradient image (the image is saved in ppm format which can be opened with e.g. IrfanView of Gimp):
The OpenCL code to generate this image:
1
2
3
4
5
6
7
8
9 | __kernel void render_kernel(__global float3* output, int width, int height)
{
constint work_item_id = get_global_id(0); /* the unique global id of the work item for the current pixel */
int x = work_item_id % width; /* x-coordinate of the pixel */
int y = work_item_id / width; /* y-coordinate of the pixel */
float fx = (float)x / (float)width; /* convert int to float in range [0-1] */
float fy = (float)y / (float)height; /* convert int to float in range [0-1] */
output[work_item_id] = (float3)(fx, fy, 0); /* simple interpolated colour gradient based on pixel coordinates */
}
|
Now let's use the OpenCL device for some ray tracing.
Ray tracing a sphere with OpenCL
We first define a Ray and a Sphere struct in the OpenCL code:A Ray has - an origin in 3D space (3 floats for x, y, z coordinates)
- a direction in 3D space (3 floats for the x, y, z coordinates of the 3D vector)
A Sphere has - a radius,
- a position in 3D space (3 floats for x, y, z coordinates),
- an object colour (3 floats for the Red, Green and Blue channel)
- an emission colour (again 3 floats for each of the RGB channels)
1
2
3
4
5
6
7
8
9
10
11 | struct Ray{
float3 origin;
float3 dir;
};
struct Sphere{
float radius;
float3 pos;
float3 emi;
float3 color;
};
|
Camera ray generation
Rays are shot from the camera (which is in a fixed position for this tutorial) through an imaginary grid of pixels into the scene, where they intersect with 3D objects (in this case spheres). For each pixel in the image, we will generate one camera ray (also called primary rays, view rays or eye rays) and follow or trace it into the scene. For camera rays, the ray origin is the camera position and the ray direction is the vector connecting the camera and the pixel on the screen.
![]() |
| Source: Wikipedia |
The OpenCL code for generating a camera ray:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | struct Ray createCamRay(constint x_coord, constint y_coord, constint width, constint height){
float fx = (float)x_coord / (float)width; /* convert int in range [0 - width] to float in range [0-1] */
float fy = (float)y_coord / (float)height; /* convert int in range [0 - height] to float in range [0-1] */
/* calculate aspect ratio */
float aspect_ratio = (float)(width) / (float)(height);
float fx2 = (fx - 0.5f) * aspect_ratio;
float fy2 = fy - 0.5f;
/* determine position of pixel on screen */
float3 pixel_pos = (float3)(fx2, -fy2, 0.0f);
/* create camera ray*/
struct Ray ray;
ray.origin = (float3)(0.0f, 0.0f, 40.0f); /* fixed camera position */
ray.dir = normalize(pixel_pos - ray.origin);
return ray;
}
|
Ray-sphere intersection
To find the intersection of a ray with a sphere, we need the parametric equation of a line, which denotes the distance from the ray origin to the intersection point along the ray direction with the parameter "t":
intersection point = ray origin + ray direction * t
The equation of a sphere follows from the Pythagorean theorem in 3D (all points on the surface of a sphere are located at a distance of radius r from its center):
(sphere surface point - sphere center)2 = radius2
Combining both equations
(ray origin + ray direction * t)2 = radius2
and expanding the equation in a quadratic equation of form ax2 + bx + c = 0 where - a = (ray direction) . (ray direction)
- b = 2 * (ray direction) . (ray origin to sphere center)
- c = (ray origin to sphere center) . (ray origin to sphere center) - radius2
yields solutions for t (the distance to the point where the ray intersects the sphere) given by the quadratic formula−b ± √ b2− 4ac / 2a (where b2 - 4acis called the discriminant).There can be zero (ray misses sphere), one (ray grazes sphere at one point) or two solutions (ray fully intersects sphere at two points). The distance t can be positive (intersection in front of ray origin) or negative (intersection behind ray origin). The details of the mathematical derivation are explained
in this Scratch-a-Pixel article.
The ray-sphere intersection algorithm is optimised by omitting the "a" coefficient in the quadratic formula, because its value is the dot product of the normalised ray direction with itself which equals 1. Taking the square root of the discriminant (an expensive function) can only be performed when the discriminant is non-negative.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | bool intersect_sphere(conststruct Sphere* sphere, conststruct Ray* ray, float* t)
{
float3 rayToCenter = sphere->pos - ray->origin;
/* calculate coefficients a, b, c from quadratic equation */
/* float a = dot(ray->dir, ray->dir); // ray direction is normalised, dotproduct simplifies to 1 */
float b = dot(rayToCenter, ray->dir);
float c = dot(rayToCenter, rayToCenter) - sphere->radius*sphere->radius;
float disc = b * b - c; /* discriminant of quadratic formula */
/* solve for t (distance to hitpoint along ray) */
if (disc < 0.0f) return false;
else *t = b - sqrt(disc);
if (*t < 0.0f){
*t = b + sqrt(disc);
if (*t < 0.0f) return false;
}
elsereturn true;
}
|
Scene initialisation
For simplicity, in this first part of the tutorial the scene will be initialised on the device in the kernel function (in the second part the scene will be initialised on the host and passed to OpenCL which is more flexible and memory efficient, but also requires to be more careful with regards to memory alignment and the use of memory address spaces). Every work item will thus have a local copy of the scene (in this case one sphere).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | __kernel void render_kernel(__global float3* output, int width, int height)
{
constint work_item_id = get_global_id(0); /* the unique global id of the work item for the current pixel */
int x_coord = work_item_id % width; /* x-coordinate of the pixel */
int y_coord = work_item_id / width; /* y-coordinate of the pixel */
/* create a camera ray */
struct Ray camray = createCamRay(x_coord, y_coord, width, height);
/* create and initialise a sphere */
struct Sphere sphere1;
sphere1.radius = 0.4f;
sphere1.pos = (float3)(0.0f, 0.0f, 3.0f);
sphere1.color = (float3)(0.9f, 0.3f, 0.0f);
/* intersect ray with sphere */
float t = 1e20;
intersect_sphere(&sphere1, &camray, &t);
/* if ray misses sphere, return background colour
background colour is a blue-ish gradient dependent on image height */
if (t > 1e19){
output[work_item_id] = (float3)(fy * 0.1f, fy * 0.3f, 0.3f);
return;
}
/* if ray hits the sphere, it will return the sphere colour*/
output[work_item_id] = sphere1.color;
}
|
Now we've got everything we need to start ray tracing! Let's begin with a plain colour sphere. When the ray misses the sphere, the background colour is returned:
A more interesting sphere with cosine-weighted colours, giving the impression of front lighting.
To achieve this effect we need to calculate the angle between the ray hitting the sphere surface and the normal at that point. The sphere normal at a specific intersection point on the surface is just the normalised vector (with unit length) going from the sphere center to that intersection point.
1
2
3
4
5 | float3 hitpoint = camray.origin + camray.dir * t;
float3 normal = normalize(hitpoint - sphere1.pos);
float cosine_factor = dot(normal, camray.dir) * -1.0f;
output[work_item_id] = sphere1.color * cosine_factor;
|
Adding some stripe pattern by multiplying the colour with the sine of the height:
Screen-door effect using sine functions for both x and y-directions
Showing the surface normals (calculated in the code snippet above) as colours:
Source code https://github.com/straaljager/OpenCL-path-tracing-tutorial-2-Part-1-Raytracing-a-sphereDownload demo (works on AMD, Nvidia and Intel)
The executable demo will render the above images.
https://github.com/straaljager/OpenCL-path-tracing-tutorial-2-Part-1-Raytracing-a-sphere/releases/tag/1.0Part 2: Path tracing spheres
Very quick overview of ray tracing and path tracing
The following section covers the background of the ray tracing process in a very simplified way, but should be sufficient to understand the code in this tutorial. Scratch-a-Pixel provides a much more detailed explanation of ray tracing.
Ray tracing is a general term that encompasses ray casting, Whitted ray tracing, distribution ray tracing and path tracing. So far, we have only traced rays from the camera (so called "camera rays", "eye rays" or "primary rays") into the scene, a process called ray casting, resulting in plainly coloured images with no lighting. In order to achieve effects like shadows and reflections, new rays must be generated at the points where the camera rays intersect with the scene. These secondary rays can be shadow rays, reflection rays, transmission rays (for refractions), ambient occlusion rays or diffuse interreflection rays (for indirect lighting/global illumination). For example, shadow rays used for direct lighting are generated to point directly towards a light source while reflection rays are pointed in (or near) the direction of the reflection vector. For now we will skip direct lighting to generate shadows and go straight to path tracing, which is strangely enough easier to code, creates more realistic and prettier pictures and is just more fun.
In (plain) path tracing, rays are shot from the camera and bounce off the surface of scene objects in a random direction (like a high-energy bouncing ball), forming a chain of random rays connected together into a path. If the path hits a light emitting object such as a light source, it will return a colour which depends on the surface colours of all the objects encountered so far along the path, the colour of the light emitters, the angles at which the path hit a surface and the angles at which the path bounced off a surface. These ideas form the essence of the "rendering equation", proposed in a paper with the same name by Jim Kajiya in 1986.
Since the directions of the rays in a path are generated randomly, some paths will hit a light source while others won't, resulting in noise ("variance" in statistics due to random sampling). The noise can be reduced by shooting many random paths per pixel (= taking many samples) and averaging the results.
Implementation of (plain) path tracing in OpenCL
The code for the path tracer is based on smallpt from Kevin Beason and is largely the same as the ray tracer code from part 1 of this tutorial, with some important differences on the host side:
- the scene is initialised on the host (CPU) side, which requires a host version of the Sphere struct. Correct memory alignment in the host struct is very important to avoid shifting of values and wrongly initialised variables in the OpenCL struct, especially when using OpenCL's built-in data types such as float3 and float4. If necessary, the struct should be padded with dummy variables to ensure memory alignment (the total size of the struct must be a multiple of the size of float4).
1
2
3
4
5
6
7
8
9
10 | struct Sphere
{
cl_float radius;
cl_float dummy1;
cl_float dummy2;
cl_float dummy3;
cl_float3 position;
cl_float3 color;
cl_float3 emission;
};
|
- the scene (an array of spheres) is copied from the host to the OpenCL device into global memory (using CL_MEM_READ_WRITE) or constant memory (using CL_MEM_READ_ONLY)
1
2
3
4
5
6
7
8
9 | // initialise scene
constint sphere_count = 9;
Sphere cpu_spheres[sphere_count];
initScene(cpu_spheres);
// Create buffers on the OpenCL device for the image and the scene
cl_output = Buffer(context, CL_MEM_WRITE_ONLY, image_width * image_height * sizeof(cl_float3));
cl_spheres = Buffer(context, CL_MEM_READ_ONLY, sphere_count * sizeof(Sphere));
queue.enqueueWriteBuffer(cl_spheres, CL_TRUE, 0, sphere_count * sizeof(Sphere), cpu_spheres);
|
- explicit memory management: once the scene is on the device, its pointer can be passed on to other device functions preceded by the keyword "__global" or "__constant".
- the host code automatically determines the local size of the kernel work group (the number of work items or "threads" per work group) by calling the OpenCL function kernel.getWorkGroupInfo(device)
The actual path tracing function
- iterative path tracing function: since OpenCL does not support recursion, the trace() function traces paths iteratively (instead of recursively) using a loop with a fixed number of bounces (iterations), representing path depth.
- each path starts off with an "accumulated colour" initialised to black and a "mask colour" initialised to pure white. The mask colour "collects" surface colours along its path by multiplication. The accumulated colour accumulates light from emitters along its path by adding emitted colours multiplied by the mask colour.
- generating random ray directions: new rays start at the hitpoint and get shot in a random direction by sampling a random point on the hemisphere above the surface hitpoint. For each new ray, a local orthogonal uvw-coordinate system and two random numbers are generated: one to pick a random value on the horizon for the azimuth, the other for the altitude (with the zenith being the highest point)
- diffuse materials: the code for this tutorial only supports diffuse materials, which reflect incident light almost uniformly in all directions (in the hemisphere above the hitpoint)
- cosine-weighted importance sampling: because diffuse light reflection is not truly uniform, the light contribution from rays that are pointing away from the surface plane and closer to the surface normal is greater. Cosine-weighted importance sampling favours rays that are pointing away from the surface plane by multiplying their colour with the cosine of the angle between the surface normal and the ray direction.
- while ray tracing can get away with tracing only one ray per pixel to render a good image (more are needed for anti-aliasing and blurry effects like depth-of-field and glossy reflections), the inherently noisy nature of path tracing requires tracing of many paths per pixel (samples per pixel) and averaging the results to reduce noise to an acceptable level.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56 | float3 trace(__constant Sphere* spheres, const Ray* camray, constint sphere_count, constint* seed0, constint* seed1){
Ray ray = *camray;
float3 accum_color = (float3)(0.0f, 0.0f, 0.0f);
float3 mask = (float3)(1.0f, 1.0f, 1.0f);
for (int bounces = 0; bounces < 8; bounces++){
float t; /* distance to intersection */
int hitsphere_id = 0; /* index of intersected sphere */
/* if ray misses scene, return background colour */
if (!intersect_scene(spheres, &ray, &t, &hitsphere_id, sphere_count))
return accum_color += mask * (float3)(0.15f, 0.15f, 0.25f);
/* else, we've got a hit! Fetch the closest hit sphere */
Sphere hitsphere = spheres[hitsphere_id]; /* version with local copy of sphere */
/* compute the hitpoint using the ray equation */
float3 hitpoint = ray.origin + ray.dir * t;
/* compute the surface normal and flip it if necessary to face the incoming ray */
float3 normal = normalize(hitpoint - hitsphere.pos);
float3 normal_facing = dot(normal, ray.dir) < 0.0f ? normal : normal * (-1.0f);
/* compute two random numbers to pick a random point on the hemisphere above the hitpoint*/
float rand1 = 2.0f * PI * get_random(seed0, seed1);
float rand2 = get_random(seed0, seed1);
float rand2s = sqrt(rand2);
/* create a local orthogonal coordinate frame centered at the hitpoint */
float3 w = normal_facing;
float3 axis = fabs(w.x) > 0.1f ? (float3)(0.0f, 1.0f, 0.0f) : (float3)(1.0f, 0.0f, 0.0f);
float3 u = normalize(cross(axis, w));
float3 v = cross(w, u);
/* use the coordinte frame and random numbers to compute the next ray direction */
float3 newdir = normalize(u * cos(rand1)*rand2s + v*sin(rand1)*rand2s + w*sqrt(1.0f - rand2));
/* add a very small offset to the hitpoint to prevent self intersection */
ray.origin = hitpoint + normal_facing * EPSILON;
ray.dir = newdir;
/* add the colour and light contributions to the accumulated colour */
accum_color += mask * hitsphere.emission;
/* the mask colour picks up surface colours at each bounce */
mask *= hitsphere.color;
/* perform cosine-weighted importance sampling for diffuse surfaces*/
mask *= dot(newdir, normal_facing);
}
return accum_color;
}
|
A screenshot made with the code above (also see the screenshot at the top of this post). Notice the colour bleeding (bounced colour reflected from the floor onto the spheres), soft shadows and lighting coming from the background.
Source code
Up next
The next tutorial will cover the implementation of an interactive OpenGL viewport with a progressively refining image and an interactive camera with anti-aliasing and depth-of-field.