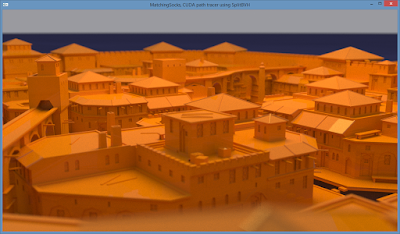
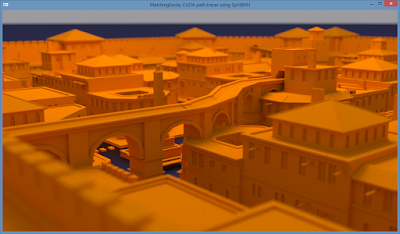
Free introductory minibook on ray tracing
Start your engines: source code for FireRays (AMD's high performance OpenCL based GPU ray tracing framework) available
And an old video from one of the developers:
Nvidia open sourced their high performance CUDA based ray tracing framework in 2009, but hasn't updated it since 2012 (presumably due to the lack of any real competition from AMD in this area) and has since focused more on developing OptiX, a CUDA based closed source ray tracing library. Intel open sourced Embree in 2011, which is being actively developed and updated with new features and performance improvements. They even released another open source high performance ray tracer for scientific visualisation called OSPRay.
Real-time path traced Quake 2
Project link with videos: http://amietia.com/q2pt.html
Full source code on Github: https://github.com/eddbiddulph/yquake2/tree/pathtracing
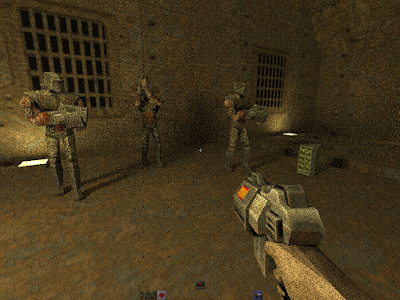 | |
| Quake 2, now with real-time indirect lighting and soft shadows |
Why Quake 2 instead of Quake 3
I chose Quake 2 because it has area lightsources and the maps were designed with multiple-bounce lighting in mind. As far as I know, Quake 3 was not designed this way and didn't even have area lightsources for the baked lighting. Plus Quake 2's static geometry was still almost entirely defined by a binary space partitioning tree (BSP) and I found that traversing a BSP is pretty easy in GLSL and seems to perform quite well, although I haven't made any comparisons to other approaches. Quake 3 has a lot more freeform geometry such as tessellated Bezier surfaces so it doesn't lend itself so well to special optimisations. I'm a big fan of both games of course :)
How the engine updates dynamic objects
All dynamic geometry is inserted into a single structure which is re-built from scratch on every frame. Each node is an axis-aligned bounding box and has a 'skip pointer' to skip over the children. I make a node for each triangle and build the structure bottom-up after sorting the leaf nodes by morton code for spatial coherence. I chose this approach because the implementation is simple both for building and traversing, the node hierarchy is quite flexible, and building is fast although the whole CPU side is single-threaded for now (mostly because Quake 2 is single-threaded of course). I'm aware that the lack of ordered traversal results in many more ray-triangle intersection tests than are necessary, but there is little divergence and low register usage since the traversal is stackless.
How to keep noise to a minimum when dealing with so many lights
The light selection is a bit more tricky. I divided lightsources into two categories - regular and 'skyportals'. A skyportal is just a light-emitting surface from the original map data which has a special texture applied, which indicates to the game that the skybox should be drawn there. Each leaf in the BSP has two lists of references to lightsources. The first list references regular lightsources which are potentially visible from the leaf according to the PVS (potentially visible set) tables. The second list references skyportals which are contained within the leaf. At an intersection point the first list is used to trace shadow rays and make explicit samples of lightsources, and the second list is used to check if the intersection point is within a skyportal surface. If it's within a skyportal then there is a contribution of light from the sky. This way I can perform a kind of offline multiple importance sampling (MIS) because skyportals are generally much larger than regular lights. For regular lights of course I use importance sampling, but I believe the weight I use is more approximate than usual because it's calculated always from the center of the lightsource rather than from the real sample position on the light.
One big point about the lights right now is that the pointlights that the original game used are being added as 4 triangular lightsources arranged in a tetrahedron so they tend to make quite a performance hit. I'd like to try adding a whole new type of lightsource such as a spherical light to see if that works out better.
Ray tracing specific optimisations
I'm making explicit light samples by tracing shadow rays directly towards points on the lightsources. MIS isn't being performed in the shader, but I'm deciding offline whether a lightsource should be sampled explicitly or implicitly.
Which parts of the rendering process use rasterisation
I use hardware rasterisation only for the primary rays and perform the raytracing in the same pass for the following reasons:
- Translucent surfaces can be lit and can receive shadows identically to all other surfaces.
- Hardware anti-aliasing can be used, of course.
- Quake 2 sorts translucent BSP surfaces and draws them in a second pass, but it doesn't do this for entities (the animated objects) so I would need to change that design and I consider this too intrusive and likely to break something. One of my main goals was to preserve the behaviour of Q2's own renderer.
- I'm able to eliminate overdraw by making a depth-only pre-pass which even uses the same GL buffers that the raytracer uses so it has little overhead except for a trick that I had to make since I packed the three 16-bit triangle indices for the raytracer into two 32-bit elements (this was necessary due to OpenGL limitations on texture buffer objects).
- It's nice that I don't need to manage framebuffer stuff and design a good g-buffer format.
The important project files containing the path tracing code
If you want to take a look at the main parts that I wrote, stick to src/client/refresh/r_pathtracing.c and src/client/refresh/pathtracer.glsl. The rest of my changes were mostly about adding various GL extensions and hooking in my stuff to the old refresh subsystem (Quake 2's name for the renderer). I apologise that r_pathtracing.c is such a huge file, but I did try to comment it nicely and refactoring is already on my huge TODO list. The GLSL file is converted into a C header at build time by stringifyshaders.sh which is at the root of the codebase.
More interesting tidbits
- This whole project is only made practical by the fact that the BSP files still contain surface emission data despite the game itself making no use of it at all. This is clearly a by-product of keeping the map-building process simple, and it's a very fortunate one!
- The designers of the original maps sometimes placed pointlights in front of surface lights to give the appearence that they are glowing or emitting light at their sides like a fluorescent tube diffuser. This looks totally weird in my pathtracer so I have static pointlights disabled by default. They also happen to go unused by the original game, so it's also fortunate that they still exist among the map data.
- The weapon that is viewed in first-person is drawn with a 'depth hack' (it's literally called RF_DEPTHHACK), in which the range of depth values is reduced to prevent the weapon poking in to walls. Unfortunately the pathtracer's representation would still poke in to walls because it needs the triangles in worldspace, and this would cause the tip of the weapon to turn black (completely in shadow). I worked around this by 'virtually' scaling down the weapon for the pathtracer. This is one of the many ways in which raytracing turns out to be tricky for videogames, but I'm sure there can always be elegant solutions.
- on Windows, follow the steps under section 2.3 in the readme file (link: https://github.com/eddbiddulph/yquake2/blob/pathtracing/README). Lots of websites still offer the Quake 2 demo for download (e.g. http://www.ausgamers.com/files/download/314/quake-2-demo)
- download and unzip the Yamagi Quake 2 source code with path tracing from https://github.com/eddbiddulph/yquake2
- following the steps under section 2.6 of the readme file, download and extract the premade MinGW build environment, run MSYS32, navigate to the source directory with the makefile, "make" the release build and replace the files "q2ded.exe", "quake2.exe" and "baseq2\game.dll" in the Quake 2 game installation with the freshly built ones
- start the game by double clicking "quake2", open the Quake2 console with the ~ key (under the ESC key), type "gl_pt_enable 1", hit Enter and the ~ key to close the console
- the game should now run with path tracing
Edd also said he's also planning to add new special path tracing effects (such as light emitting particles from the railgun) and implementing more optimisations to reduce the path tracing noise.
GPU path tracing tutorial 4: Optimised BVH building, faster traversal and intersection kernels and HDR environment lighting
- wiki.blender.org/index.php/Dev:Source/Render/Cycles/BVH
- github.com/doug65536/blender/blob/master/intern/cycles/kernel/kernel_bvh.h
- github.com/doug65536/blender/blob/master/intern/cycles/kernel/kernel_bvh_traversal.h
- SplitBVHBuilder.cpp contains the algorithm for building BVH with spatial splits
- CudaBVH.cppshows the particular layout in which the BVH nodes are stored and Woop's triangle transformation method
- renderkernel.cudemonstrates two methods of ray/triangle intersection: a regular ray/triangle intersection algorithm similar to the one in GPU path tracing tutorial 3, denoted as DEBUGintersectBVHandTriangles() and a method using Woop's ray/triangle intersection named intersectBVHandTriangles()
github.com/straaljager/GPU-path-tracing-tutorial-4/releases
OpenCL path tracing tutorial 1: Firing up OpenCL
- Platform: which vendor (AMD/Nvidia/Intel)
- Device: CPU, GPU, APU or integrated GPU
- Context: the runtime interface between the host (CPU) and device (GPU or CPU) which manages all the OpenCL resources (programs, kernels, command queue, buffers). It receives and distributes kernels and transfers data.
- Program: the entire OpenCL program (one or more kernels and device functions)
- Kernel: the starting point into the OpenCL program, analogous to the main() function in a CPU program. Kernels are called from the host (CPU). They represent the basic units of executable code that run on an OpenCL device and are preceded by the keyword "__kernel"
- Command queue: the command queue allows kernel execution commands to be sent to the device (execution can be in-order or out-of-order)
- Memory objects: buffers and images
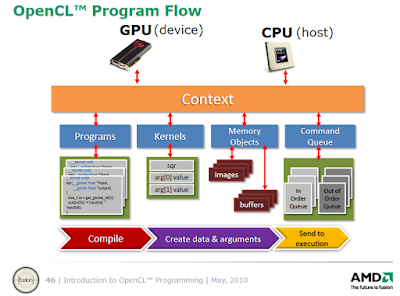 |
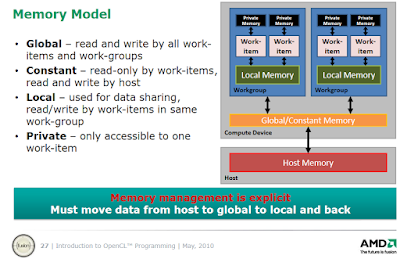
| OpenCL execution model |
- Global memory (similar to RAM): the largest but also slowest form of memory, can be read and written to by all work items (threads) and all work groups on the device and can also be read/written by the host (CPU).
- Constant memory: a small chunk of global memory on the device, can be read by all work items on the device (but not written to) and can be read/written by the host. Constant memory is slightly faster than global memory.
- Local memory (similar to cache memory on the CPU): memory shared among work items in the same work group (work items executing together on the same compute unit are grouped into work groups). Local memory allows work items belonging to the same work group to share results. Local memory is much faster than global memory (up to 100x).
- Private memory (similar to registers on the CPU): the fastest type of memory. Each work item (thread) has a tiny amount of private memory to store intermediate results that can only be used by that work item
First OpenCL program
In a nutshell, what happens is the following:
- Initialise the OpenCL computing environment: create a platform, device, context, command queue, program and kernel and set up the kernel arguments
- Create two floating point number arrays on the host side and copy them to the OpenCL device
- Make OpenCL perform the computation in parallel (by determining global and local worksizes and launching the kernel)
- Copy the results of the computation from the device to the host
- Print the results to the console
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
// by Sam Lapere, 2016, http://raytracey.blogspot.com
// Code based on http://simpleopencl.blogspot.com/2013/06/tutorial-simple-start-with-opencl-and-c.html
#include <iostream>
#include <vector>
#include <CL\cl.hpp> // main OpenCL include file
usingnamespace cl;
usingnamespace std;
void main()
{
// Find all available OpenCL platforms (e.g. AMD, Nvidia, Intel)
vector<Platform> platforms;
Platform::get(&platforms);
// Show the names of all available OpenCL platforms
cout << "Available OpenCL platforms: \n\n";
for (unsignedint i = 0; i < platforms.size(); i++)
cout << "\t"<< i + 1 << ": "<< platforms[i].getInfo<CL_PLATFORM_NAME>() << endl;
// Choose and create an OpenCL platform
cout << endl << "Enter the number of the OpenCL platform you want to use: ";
unsignedint input = 0;
cin >> input;
// Handle incorrect user input
while (input < 1 || input > platforms.size()){
cin.clear(); //clear errors/bad flags on cin
cin.ignore(cin.rdbuf()->in_avail(), '\n'); // ignores exact number of chars in cin buffer
cout << "No such platform."<< endl << "Enter the number of the OpenCL platform you want to use: ";
cin >> input;
}
Platform platform = platforms[input - 1];
// Print the name of chosen OpenCL platform
cout << "Using OpenCL platform: \t"<< platform.getInfo<CL_PLATFORM_NAME>() << endl;
// Find all available OpenCL devices (e.g. CPU, GPU or integrated GPU)
vector<Device> devices;
platform.getDevices(CL_DEVICE_TYPE_ALL, &devices);
// Print the names of all available OpenCL devices on the chosen platform
cout << "Available OpenCL devices on this platform: "<< endl << endl;
for (unsignedint i = 0; i < devices.size(); i++)
cout << "\t"<< i + 1 << ": "<< devices[i].getInfo<CL_DEVICE_NAME>() << endl;
// Choose an OpenCL device
cout << endl << "Enter the number of the OpenCL device you want to use: ";
input = 0;
cin >> input;
// Handle incorrect user input
while (input < 1 || input > devices.size()){
cin.clear(); //clear errors/bad flags on cin
cin.ignore(cin.rdbuf()->in_avail(), '\n'); // ignores exact number of chars in cin buffer
cout << "No such device. Enter the number of the OpenCL device you want to use: ";
cin >> input;
}
Device device = devices[input - 1];
// Print the name of the chosen OpenCL device
cout << endl << "Using OpenCL device: \t"<< device.getInfo<CL_DEVICE_NAME>() << endl << endl;
// Create an OpenCL context on that device.
// the context manages all the OpenCL resources
Context context = Context(device);
///////////////////
// OPENCL KERNEL //
///////////////////
// the OpenCL kernel in this tutorial is a simple program that adds two float arrays in parallel
// the source code of the OpenCL kernel is passed as a string to the host
// the "__global" keyword denotes that "global" device memory is used, which can be read and written
// to by all work items (threads) and all work groups on the device and can also be read/written by the host (CPU)
constchar* source_string =
" __kernel void parallel_add(__global float* x, __global float* y, __global float* z){ "
" const int i = get_global_id(0); "// get a unique number identifying the work item in the global pool
" z[i] = y[i] + x[i]; "// add two arrays
"}";
// Create an OpenCL program by performing runtime source compilation
Program program = Program(context, source_string);
// Build the program and check for compilation errors
cl_int result = program.build({ device }, "");
if (result) cout << "Error during compilation! ("<< result << ")"<< endl;
// Create a kernel (entry point in the OpenCL source program)
// kernels are the basic units of executable code that run on the OpenCL device
// the kernel forms the starting point into the OpenCL program, analogous to main() in CPU code
// kernels can be called from the host (CPU)
Kernel kernel = Kernel(program, "parallel_add");
// Create input data arrays on the host (= CPU)
constint numElements = 10;
float cpuArrayA[numElements] = { 0.0f, 1.0f, 2.0f, 3.0f, 4.0f, 5.0f, 6.0f, 7.0f, 8.0f, 9.0f };
float cpuArrayB[numElements] = { 0.1f, 0.2f, 0.3f, 0.4f, 0.5f, 0.6f, 0.7f, 0.8f, 0.9f, 1.0f };
float cpuOutput[numElements] = {}; // empty array for storing the results of the OpenCL program
// Create buffers (memory objects) on the OpenCL device, allocate memory and copy input data to device.
// Flags indicate how the buffer should be used e.g. read-only, write-only, read-write
Buffer clBufferA = Buffer(context, CL_MEM_READ_ONLY | CL_MEM_COPY_HOST_PTR, numElements * sizeof(cl_int), cpuArrayA);
Buffer clBufferB = Buffer(context, CL_MEM_READ_ONLY | CL_MEM_COPY_HOST_PTR, numElements * sizeof(cl_int), cpuArrayB);
Buffer clOutput = Buffer(context, CL_MEM_WRITE_ONLY, numElements * sizeof(cl_int), NULL);
// Specify the arguments for the OpenCL kernel
// (the arguments are __global float* x, __global float* y and __global float* z)
kernel.setArg(0, clBufferA); // first argument
kernel.setArg(1, clBufferB); // second argument
kernel.setArg(2, clOutput); // third argument
// Create a command queue for the OpenCL device
// the command queue allows kernel execution commands to be sent to the device
CommandQueue queue = CommandQueue(context, device);
// Determine the global and local number of "work items"
// The global work size is the total number of work items (threads) that execute in parallel
// Work items executing together on the same compute unit are grouped into "work groups"
// The local work size defines the number of work items in each work group
// Important: global_work_size must be an integer multiple of local_work_size
std::size_t global_work_size = numElements;
std::size_t local_work_size = 10; // could also be 1, 2 or 5 in this example
// when local_work_size equals 10, all ten number pairs from both arrays will be added together in one go
// Launch the kernel and specify the global and local number of work items (threads)
queue.enqueueNDRangeKernel(kernel, NULL, global_work_size, local_work_size);
// Read and copy OpenCL output to CPU
// the "CL_TRUE" flag blocks the read operation until all work items have finished their computation
queue.enqueueReadBuffer(clOutput, CL_TRUE, 0, numElements * sizeof(cl_float), cpuOutput);
// Print results to console
for (int i = 0; i < numElements; i++)
cout << cpuArrayA[i] << " + "<< cpuArrayB[i] << " = "<< cpuOutput[i] << endl;
system("PAUSE");
}
https://github.com/straaljager/OpenCL-path-tracing-tutorial-1-Getting-started
Compiling instructions(for Visual Studio on Windows)
- Start an empty Console project in Visual Studio (any recent version should work, including Express and Community) and set to Release mode
- Add the SDK include path to the "Additional Include Directories" (e.g. "C:\Program Files (x86)\AMD APP SDK\2.9-1\include")
- In Linker > Input, add "opencl.lib" to "Additional Dependencies" and add the OpenCL lib path to "Additional Library Directories" (e.g. "C:\Program Files (x86)\AMD APP SDK\2.9-1\lib\x86")
- Add the main.cpp file (or create a new file and paste the code) and build the project
https://github.com/straaljager/OpenCL-path-tracing-tutorial-1-Getting-started/releases/tag/v1.0
It runs on CPUs and/or GPUs from AMD, Nvidia and Intel.
Useful References
- "A gentle introduction to OpenCL":
http://www.drdobbs.com/parallel/a-gentle-introduction-to-opencl/231002854
- "Simple start with OpenCL":
http://simpleopencl.blogspot.co.nz/2013/06/tutorial-simple-start-with-opencl-and-c.html
- Anteru's blogpost, Getting started with OpenCL (uses old OpenCL API)
https://anteru.net/blog/2012/11/03/2009/index.html
- AMD introduction to OpenCL programming:
http://amd-dev.wpengine.netdna-cdn.com/wordpress/media/2013/01/Introduction_to_OpenCL_Programming-201005.pdf
Up next
In the next tutorial we'll start rendering an image with OpenCL.
OpenCL path tracing tutorial 2: path tracing spheres
- x-coordinate: divide by the image width and take the remainder
- y-coordinate: divide by the image width
2
3
4
5
6
7
8
9
{
constint work_item_id = get_global_id(0); /* the unique global id of the work item for the current pixel */
int x = work_item_id % width; /* x-coordinate of the pixel */
int y = work_item_id / width; /* y-coordinate of the pixel */
float fx = (float)x / (float)width; /* convert int to float in range [0-1] */
float fy = (float)y / (float)height; /* convert int to float in range [0-1] */
output[work_item_id] = (float3)(fx, fy, 0); /* simple interpolated colour gradient based on pixel coordinates */
}
- an origin in 3D space (3 floats for x, y, z coordinates)
- a direction in 3D space (3 floats for the x, y, z coordinates of the 3D vector)
- a radius,
- a position in 3D space (3 floats for x, y, z coordinates),
- an object colour (3 floats for the Red, Green and Blue channel)
- an emission colour (again 3 floats for each of the RGB channels)
2
3
4
5
6
7
8
9
10
11
float3 origin;
float3 dir;
};
struct Sphere{
float radius;
float3 pos;
float3 emi;
float3 color;
};
Camera ray generation
 |
| Source: Wikipedia |
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
float fx = (float)x_coord / (float)width; /* convert int in range [0 - width] to float in range [0-1] */
float fy = (float)y_coord / (float)height; /* convert int in range [0 - height] to float in range [0-1] */
/* calculate aspect ratio */
float aspect_ratio = (float)(width) / (float)(height);
float fx2 = (fx - 0.5f) * aspect_ratio;
float fy2 = fy - 0.5f;
/* determine position of pixel on screen */
float3 pixel_pos = (float3)(fx2, -fy2, 0.0f);
/* create camera ray*/
struct Ray ray;
ray.origin = (float3)(0.0f, 0.0f, 40.0f); /* fixed camera position */
ray.dir = normalize(pixel_pos - ray.origin);
return ray;
}
Ray-sphere intersection
- a = (ray direction) . (ray direction)
- b = 2 * (ray direction) . (ray origin to sphere center)
- c = (ray origin to sphere center) . (ray origin to sphere center) - radius2
There can be zero (ray misses sphere), one (ray grazes sphere at one point) or two solutions (ray fully intersects sphere at two points). The distance t can be positive (intersection in front of ray origin) or negative (intersection behind ray origin). The details of the mathematical derivation are explained in this Scratch-a-Pixel article.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
{
float3 rayToCenter = sphere->pos - ray->origin;
/* calculate coefficients a, b, c from quadratic equation */
/* float a = dot(ray->dir, ray->dir); // ray direction is normalised, dotproduct simplifies to 1 */
float b = dot(rayToCenter, ray->dir);
float c = dot(rayToCenter, rayToCenter) - sphere->radius*sphere->radius;
float disc = b * b - c; /* discriminant of quadratic formula */
/* solve for t (distance to hitpoint along ray) */
if (disc < 0.0f) return false;
else *t = b - sqrt(disc);
if (*t < 0.0f){
*t = b + sqrt(disc);
if (*t < 0.0f) return false;
}
elsereturn true;
}
Scene initialisation
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
{
constint work_item_id = get_global_id(0); /* the unique global id of the work item for the current pixel */
int x_coord = work_item_id % width; /* x-coordinate of the pixel */
int y_coord = work_item_id / width; /* y-coordinate of the pixel */
/* create a camera ray */
struct Ray camray = createCamRay(x_coord, y_coord, width, height);
/* create and initialise a sphere */
struct Sphere sphere1;
sphere1.radius = 0.4f;
sphere1.pos = (float3)(0.0f, 0.0f, 3.0f);
sphere1.color = (float3)(0.9f, 0.3f, 0.0f);
/* intersect ray with sphere */
float t = 1e20;
intersect_sphere(&sphere1, &camray, &t);
/* if ray misses sphere, return background colour
background colour is a blue-ish gradient dependent on image height */
if (t > 1e19){
output[work_item_id] = (float3)(fy * 0.1f, fy * 0.3f, 0.3f);
return;
}
/* if ray hits the sphere, it will return the sphere colour*/
output[work_item_id] = sphere1.color;
}
Running the ray tracer
Now we've got everything we need to start ray tracing! Let's begin with a plain colour sphere. When the ray misses the sphere, the background colour is returned:
A more interesting sphere with cosine-weighted colours, giving the impression of front lighting.
To achieve this effect we need to calculate the angle between the ray hitting the sphere surface and the normal at that point. The sphere normal at a specific intersection point on the surface is just the normalised vector (with unit length) going from the sphere center to that intersection point.
2
3
4
5
float3 normal = normalize(hitpoint - sphere1.pos);
float cosine_factor = dot(normal, camray.dir) * -1.0f;
output[work_item_id] = sphere1.color * cosine_factor;
Adding some stripe pattern by multiplying the colour with the sine of the height:
Screen-door effect using sine functions for both x and y-directions
Showing the surface normals (calculated in the code snippet above) as colours:
Source code
https://github.com/straaljager/OpenCL-path-tracing-tutorial-2-Part-1-Raytracing-a-sphere
Download demo (works on AMD, Nvidia and Intel)
The executable demo will render the above images.
https://github.com/straaljager/OpenCL-path-tracing-tutorial-2-Part-1-Raytracing-a-sphere/releases/tag/1.0
2
3
4
5
6
7
8
9
10
{
cl_float radius;
cl_float dummy1;
cl_float dummy2;
cl_float dummy3;
cl_float3 position;
cl_float3 color;
cl_float3 emission;
};
2
3
4
5
6
7
8
9
constint sphere_count = 9;
Sphere cpu_spheres[sphere_count];
initScene(cpu_spheres);
// Create buffers on the OpenCL device for the image and the scene
cl_output = Buffer(context, CL_MEM_WRITE_ONLY, image_width * image_height * sizeof(cl_float3));
cl_spheres = Buffer(context, CL_MEM_READ_ONLY, sphere_count * sizeof(Sphere));
queue.enqueueWriteBuffer(cl_spheres, CL_TRUE, 0, sphere_count * sizeof(Sphere), cpu_spheres);
The actual path tracing function
- while ray tracing can get away with tracing only one ray per pixel to render a good image (more are needed for anti-aliasing and blurry effects like depth-of-field and glossy reflections), the inherently noisy nature of path tracing requires tracing of many paths per pixel (samples per pixel) and averaging the results to reduce noise to an acceptable level.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
Ray ray = *camray;
float3 accum_color = (float3)(0.0f, 0.0f, 0.0f);
float3 mask = (float3)(1.0f, 1.0f, 1.0f);
for (int bounces = 0; bounces < 8; bounces++){
float t; /* distance to intersection */
int hitsphere_id = 0; /* index of intersected sphere */
/* if ray misses scene, return background colour */
if (!intersect_scene(spheres, &ray, &t, &hitsphere_id, sphere_count))
return accum_color += mask * (float3)(0.15f, 0.15f, 0.25f);
/* else, we've got a hit! Fetch the closest hit sphere */
Sphere hitsphere = spheres[hitsphere_id]; /* version with local copy of sphere */
/* compute the hitpoint using the ray equation */
float3 hitpoint = ray.origin + ray.dir * t;
/* compute the surface normal and flip it if necessary to face the incoming ray */
float3 normal = normalize(hitpoint - hitsphere.pos);
float3 normal_facing = dot(normal, ray.dir) < 0.0f ? normal : normal * (-1.0f);
/* compute two random numbers to pick a random point on the hemisphere above the hitpoint*/
float rand1 = 2.0f * PI * get_random(seed0, seed1);
float rand2 = get_random(seed0, seed1);
float rand2s = sqrt(rand2);
/* create a local orthogonal coordinate frame centered at the hitpoint */
float3 w = normal_facing;
float3 axis = fabs(w.x) > 0.1f ? (float3)(0.0f, 1.0f, 0.0f) : (float3)(1.0f, 0.0f, 0.0f);
float3 u = normalize(cross(axis, w));
float3 v = cross(w, u);
/* use the coordinte frame and random numbers to compute the next ray direction */
float3 newdir = normalize(u * cos(rand1)*rand2s + v*sin(rand1)*rand2s + w*sqrt(1.0f - rand2));
/* add a very small offset to the hitpoint to prevent self intersection */
ray.origin = hitpoint + normal_facing * EPSILON;
ray.dir = newdir;
/* add the colour and light contributions to the accumulated colour */
accum_color += mask * hitsphere.emission;
/* the mask colour picks up surface colours at each bounce */
mask *= hitsphere.color;
/* perform cosine-weighted importance sampling for diffuse surfaces*/
mask *= dot(newdir, normal_facing);
}
return accum_color;
}
A screenshot made with the code above (also see the screenshot at the top of this post). Notice the colour bleeding (bounced colour reflected from the floor onto the spheres), soft shadows and lighting coming from the background.
https://github.com/straaljager/OpenCL-path-tracing-tutorial-2-Part-2-Path-tracing-spheres
Downloadable demo (for AMD, Nvidia and Intel platforms, Windows only)
https://github.com/straaljager/OpenCL-path-tracing-tutorial-2-Part-2-Path-tracing-spheres/releases/tag/1.0
Useful resources
- Scratch-a-pixel is an excellent free online resource to learn about the theory behind ray tracing and path tracing. Many code samples (in C++) are also provided. This article gives a great introduction to global illumination and path tracing.
- smallpt by Kevin Beason is a great little CPU path tracer in 100 lines code. It of formed the inspiration for the Cornell box scene and for many parts of the OpenCL code
Wanted: GPU rendering developers
We are currently looking for excellent developers with experience in GPU rendering (path tracing) for a new project.
Our ideal candidates have either a:
- Bachelor in Computer Science, Computer/Software Engineering or Physics with a minimum of 2 years of work experience in a relevant field, or
- Master in Computer Science, Computer/Software Engineering or Physics, or
- PhD in a relevant field
Self-taught programmers are encouraged to apply if they meet the following requirements:
- you breathe rendering and have Monte Carlo simulations running through your blood
- you have a copy of PBRT (www.pbrt.org, version 3 was released just last week) on your bedside table
- provable experience working with open source rendering frameworks such as PBRT, LuxRender, Cycles, AMD RadeonRays or with a commercial renderer will earn you extra brownie points
- 5+ years of experience with C++
- experience with CUDA or OpenCL
- experience with version control systems and working on large projects
- proven rendering track record (publications, Github projects, blog)
Other requirements:
- insatiable hunger to innovate
- a "can do" attitude
- strong work ethic and focus on results
- continuous self-learner
- work well in a team
- work independently and able to take direction
- ability to communicate effectively
- comfortable speaking English
- own initiatives and original ideas are highly encouraged
- willing to relocate to New Zealand
What we offer:
- unique location in one of the most beautiful and greenest countries in the world
- be part of a small, high-performance team
- competitive salary
- jandals, marmite and hokey pokey ice cream
For more information, contact me at sam.lapere@live.be
If you are interested, send your CV and cover letter to sam.lapere@live.be. Applications will close on 16 December or when we find the right people. (update: spots are filling up quickly so we advanced the closing date with five days)
OpenCL path tracing tutorial 3: OpenGL viewport, interactive camera and defocus blur
Part 1Setting up an OpenGL window
https://github.com/straaljager/OpenCL-path-tracing-tutorial-3-Part-1
Part 2Adding an interactive camera, depth of field and progressive rendering
https://github.com/straaljager/OpenCL-path-tracing-tutorial-3-Part-2
Thanks to Erich Loftis and Brandon Miles for useful tips on improving the generation of random numbers in OpenCL to avoid the distracting artefacts (showing up as a sawtooth pattern) when using defocus blur (still not perfect but much better than before).
The next tutorial will cover rendering of triangles and triangle meshes.
Virtual reality
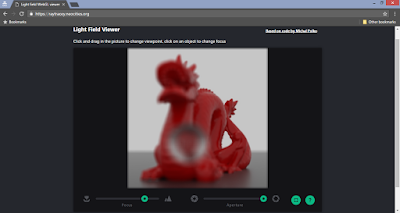
Practical light field rendering tutorial with Cycles
 |
| Bullet time in The Matrix (1999) |
Rendering the light field
Rendering a light field is actually surprisingly easy with Blender's Cycles and doesn't require much technical expertise (besides knowing how to build the plugins). For this tutorial, we'll use a couple of open source plug-ins:
 |
| 3-by-3 camera grid with their overlapping frustrums |
This plugin takes in all the images generated by the first plug-in and compresses them by keeping some keyframes and encoding the delta in the remaining intermediary frames. The viewer is WebGL based and makes use of virtual texturing (similar to Carmack's mega-textures) for fast, on-the-fly reconstruction of new viewpoints from pre-rendered viewpoints (via hardware accelerated bilinear interpolation on the GPU).
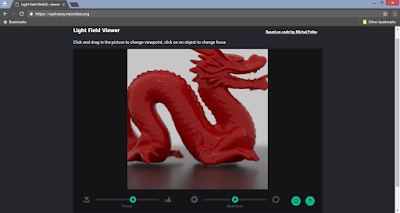
Results and Live Demo
A live online demo of the light field with the dragon can be seen here:
Towards real-time path tracing: An Efficient Denoising Algorithm for Global Illumination
Abstract
We propose a hybrid ray-tracing/rasterization strategy for realtime rendering enabled by a fast new denoising method. We factor global illumination into direct light at rasterized primary surfaces and two indirect lighting terms, each estimated with one pathtraced sample per pixel. Our factorization enables efficient (biased) reconstruction by denoising light without blurring materials. We demonstrate denoising in under 10 ms per 1280×720 frame, compare results against the leading offline denoising methods, and include a supplement with source code, video, and data.
Abstract
We introduce a reconstruction algorithm that generates a temporally stable sequence of images from one path-per-pixel global illumination. To handle such noisy input, we use temporal accumulation to increase the effective sample count and spatiotemporal luminance variance estimates to drive a hierarchical, image-space wavelet filter. This hierarchy allows us to distinguish between noise and detail at multiple scales using luminance variance.
Physically-based light transport is a longstanding goal for real-time computer graphics. While modern games use limited forms of ray tracing, physically-based Monte Carlo global illumination does not meet their 30 Hz minimal performance requirement. Looking ahead to fully dynamic, real-time path tracing, we expect this to only be feasible using a small number of paths per pixel. As such, image reconstruction using low sample counts is key to bringing path tracing to real-time. When compared to prior interactive reconstruction filters, our work gives approximately 10x more temporally stable results, matched references images 5-47% better (according to SSIM), and runs in just 10 ms (+/- 15%) on modern graphics hardware at 1920x1080 resolution.
Freedom of noise: Nvidia releases OptiX 5.0 with royalty-free AI denoiser
 |
| The OptiX denoiser works great for glass and dark, indirectly lit areas |
While in general the denoiser does a fantastic job, it's not yet optimised to deal with areas that converge fast, and in some instances overblurs and fails to preserve texture detail as shown in the screen grab below (perhaps this can be solved with more training for the machine learning):
 |
| Overblurring of textures |
Some videos of the denoiser in action in Optix, V-Ray, Redshift and Clarisse:
Optix 5.0: youtu.be/l-5NVNgT70U
Iray: youtu.be/yPJaWvxnYrg
V-Ray 4.0: youtu.be/nvA4GQAPiTc
Redshift: youtu.be/ofcCQdIZAd8 (and a post from Redshift's Panos explaining the implementation in Redshift)
ClarisseFX: youtu.be/elWx5d7c_DI
Real-time path tracing on a 40 megapixel screen
- hand optimised BVH traversal and geometry intersection kernels
- real-time path traced diffuse global illumination
- Optix real-time AI accelerated denoising
- HDR environment map lighting
- explicit direct lighting (next event estimation)
- quasi-Monte Carlo sampling
- volume rendering
- procedural geometry
- signed distance fields raymarching
- instancing, allowing to visualize billions of dynamic molecules in real-time
- stereoscopic omnidirectional 3D rendering
- efficient loading and rendering of multi-terabyte datasets
- linear scaling across many nodes
- optimised for real-time distributed rendering on a cluster with high speed network interconnection
- ultra-low latency streaming to high resolution display walls and VR caves
- modular architecture which makes it ideal for experimenting with new rendering techniques
- optional noise and gluten free rendering
 |
| Real-time path traced scene on a 8 m by 3 m (25 by 10 ft) semi-cylindrical display, powered by seven 4K projectors (40 megapixels in total) |
Technical/Medical/Scientific 3D artists wanted
Accelerating path tracing by using the BVH as multiresolution geometry
- Skipping triangle intersection
- only ray/box intersection, better for thread divergence
TODO link to github code, propose fixes to fill holes, present benchmark results (8x speedup), get more timtams
Nvidia gearing up to unleash real-time ray tracing to the masses
One of the authors of the Physically Based Rendering books (www.pbrt.org, some say it's the bible for Monte Carlo ray tracing). Before joining Nvidia, he was working at Google with Paul Debevec on Daydream VR, light fields and Seurat (https://www.blog.google/products/google-ar-vr/experimenting-light-fields/), none of which took off in a big way for some reason.
Before Google, he worked at Intel on Larrabee, Intel's failed attempt at making a GPGPU for real-time ray tracing and rasterisation which could compete with Nvidia GPUs) and ISPC, a specialised compiler intended to extract maximum parallelism from the new Intel chips with AVX extensions. He described his time at Intel in great detail on his blog: http://pharr.org/matt/blog/2018/04/30/ispc-all.html (sounds like an awful company to work for).
Intel also bought Neoptica, Matt's startup, which was supposed to research new and interesting rendering techniques for hybrid CPU/GPU chip architectures like the PS3's Cell
Pioneering researcher in the field of real-time ray tracing from the Saarbrücken computer graphics group in Germany, who later moved to Intel and the university of Utah to work on a very high performance CPU based ray tracing frameworks such as Embree (used in Corona Render and Cycles) and Ospray.
His PhD thesis "Real-time ray tracing and interactive global illumination" from 2004, describes a real-time GI renderer running on a cluster of commodity PCs and hardware accelerated ray tracing (OpenRT) on a custom fixed function ray tracing chip (SaarCOR).
Ingo contributed a lot to the development of high quality ray tracing acceleration structures (built with the surface area heuristic).
Main author of the famous Real-time Rendering blog, who worked until recently for Autodesk. He also used to maintain the Real-time Raytracing Realm and Ray Tracing News
What connects these people is that they all have a passion for real-time ray tracing running in their blood, so having them all united under one roof is bound to give fireworks.
Chaos Group (V-Ray) announces real-time path tracer Lavina
Excerpt:
"Specialized hardware for ray casting has been attempted in the past, but has been largely unsuccessful — partly because the shading and ray casting calculations are usually closely related and having them run on completely different hardware devices is not efficient. Having both processes running inside the same GPU is what makes the RTX architecture interesting. We expect that in the coming years the RTX series of GPUs will have a large impact on rendering and will firmly establish GPU ray tracing as a technique for producing computer generated images both for off-line and real-time rendering."
The article features a new research project, called Lavina, which is essentially doing real-time ray tracing and path tracing (with reflections, refractions and one GI bounce). The video below gets seriously impressive towards the end:
Nvidia release OptiX 6.0 with support for hardware accelerated ray tracing
Unreal Engine now has real-time ray tracing and a path tracer
https://www.unrealengine.com/en-US/blog/real-time-ray-tracing-new-on-set-tools-unreal-engine-4-22
The path tracer is explained in more detail on this page: https://docs.unrealengine.com/en-us/Engine/Rendering/RayTracing/PathTracer
The following video is an incredible example of an architectural visualisation rendered with Unreal's real-time raytraced reflections and refractions:
LightTracer, the first WebGL path tracer for photorealistic rendering of complex scenes in the browser
LightHouse 2, the new OptiX based real-time GPU path tracing framework, released as open source
- Lighthouse uses Nvidia's OptiX framework, which provides state-of-the-art methods to build and traverse BVH acceleration structures, including a built-in "top level BVH" which allows for real-time animated scenes with thousands of individual meshes, practically for free.
- There are 3 manually optimised OptiX render cores:
- OptiX 5 and OptiX Prime for Maxwell and Pascal
- the new OptiX 7 for Volta and Turing
- OptiX 7 is much more low level than previous OptiX versions, creating more control for the developer, less overhead and a substantial performance boost on Turing GPUs compared to OptiX 5/6 (about 35%)
- A Turing GPU running Lighthouse 2 with OptiX 7 (with RTX support) is about 6x faster than a Pascal GPU running OptiX 5 for path tracing (you have to try it to believe it :-) )
- Lighthouse incorporates the new "blue noise" sampling method (https://eheitzresearch.wordpress.com/762-2/), which creates cleaner/less noisy looking images at low sample rates
- Lighthouse manages a full game scene graph with instances, camera, lights and materials, including the Disney BRDF (principled shader) and their parameters can be edited on-the-fly through a lightweight GUI
 | |
| 1024 real-time ray traced dragons |
 |
| 2025 lego cars, spinning in real-time |
 |
| Lighthouse 2 material test scene |
 |
| A real-time raytraced Shelby Cobra |
An old video of Sponza rendered with Lighthouse, showing off the real-time denoiser:
Lighthouse is still a work in progress, but given the fact that it handles real-time animation, offers state-of-the-art performance and is licensed under Apache 2.0, it may soon end up in professional 3D tools like Blender for fast, photorealistic previews of real-time animations. Next-gen game engine developers should also keep an eye on this.
P.S. I may release some executable demos for people who can't compile Lighthouse on their machines.
Finally...
Marbles RTX at night
Nvidia showed an improved version of their Marbles RTX demo during the RTX 3000 launch event. What makes this new demo so impressive is that it appears to handle dozens of small lights without breaking a sweat, something which is notoriously difficult for a path tracer, let alone one of the real-time kind:
Making of Marbles RTX (really fantastic):
The animation is rendered in real-time in Nvidia's Omniverse, a new collaborative platform which features noise-free real-time path tracing and is already turning some heads in the CGI industry. Nvidia now also shared the first sneak peek of Omniverse's capabilities:
... and real-time path traced gameplay:
https://twitter.com/i/status/1304091196214534145
Be sure to watch this one, because I have a feeling it will knock a few people off their rocker when it's released. I can hardly contain my excitement!
Ray Tracing Gems II book released for free
The best things in life are free they say and that's certainly true for this gem.
Download it from here:
http://www.realtimerendering.com/raytracinggems/rtg2/index.html
Nvidia Omniverse renders everything and the kitchen sink
Last week at Siggraph, Nvidia released a fascinating making-of documentary of the Nvidia GTC keynote. It contains lots of snippets showing the real-time photorealistic rendering capabilities of Omniverse.
Short version:
Extended version:
The Siggraph talk titled "Realistic digital human rendering with Omniverse RTX Renderer" is also a must-watch for anyone interested in CG humans:
https://www.nvidia.com/en-us/on-demand/session/siggraph2021-sigg21-s-09/
Nvidia Racer RTX
Well this put a smile on my face. Nvidia just announced Racer RTX, a fully real-time raytraced minigame running on their Omniverse platform on a single RTX 4000. It looks quite a few steps up from Marbles RTX, which was already exceptional in itself. The lighting and shading quality is fairly unparalleled for a real-time application. It's amazing to see how quickly this technology has progressed in the last five years and to know that this will be available to everyone (who can afford a next-gen GPU) soon. If only GTA 6 would look as good as this...